К вопросу о рациональном выборе налогоплательщика

Преамбула. Построена экономико-математическая модель поведения налогоплательщика, максимизирующего свой выигрыш путем выбора масштаба уклонения от уплаты налогов. Установлена связь между размерами средней налоговой ставки, штрафных санкций и других издержек уклонения от налогообложения с одной стороны, и стимулами экономического агента, величиной общественного богатства и уровнем коррупции с другой стороны.

В работе В. Вишневского, А. Веткина «Уклонение от уплаты налогов и рациональный вывор налогоплательщика» (Вопросы экономики. – 2004. – No 2. – С. 96–108), посвященной анализу рационального поведения налогоплательщика, авторы выдвинули очень плодотворную, на наш взгляд, идею, указав на необходимость учитывать в качестве издержек экономического субъекта, уклоняющегося от уплаты налогов, помимо ожидаемой штрафной составляющей, те комиссионные, которые он уплачивает посреднику за содействие в уходе от налогообложения и соответствующие этому уходу трансакционные издержки. Соглашаясь в целом с позицией и аргументацией В. Вишневского и А. Веткина, мы хотели бы, во-первых, уточнить некоторые аспекты рассматриваемой проблемы и, во-вторых, несколько обобщить предлагаемую ими модель с тем, чтобы получить ответы на ряд дополнительных вопросов и, в частности, на такой отнюдь не маловажный вопрос: как именно могут отразиться на уровне коррупции, а также на размерах совокупного дохода налогоплательщика те или иные меры по борьбе с уклонением от уплаты налогов?

Прежде всего, отметим, что размер создаваемой экономическим субъектом стоимости определяется его (субъекта) соответствующими стимулами, на которые непосредственное влияние оказывает государство через такие параметры, как ставка налогообложения, эффективность работы налоговых служб, вероятность наложения штрафа за уклонение от уплаты налога и его величина, а также теми возможностями, которыми располагает субъект для оказания воздействия на некоторые из этих параметров. Поэтому величину совокупного дохода следует рассматривать в качестве эндогенной величины, а не постоянной, как в модели В. Вишневского и А. Веткина.

В основу предлагаемой ниже модификации положим, как и в вышеуказанной работе, предположение о том, что, с точки зрения налогоплательщика, осуществляемые им налоговые платежи не оборачиваются для него каким бы то ни было встречным потоком общественных благ. Налог выступает для налогоплательщика исключительно в виде финансового бремени и поэтому его рациональный выбор определяется стремлением к минимизации совокупных издержек, обусловленных как уплатой налогов, так и уклонением от этой уплаты.

Будем считать, что величина всего доходасоздаваемого экономическим субъектом, зависит от объема осуществляемых им инвестиций, который мы будем обозначать буквой α. С ростом α величина дохода возрастает, поэтому считаем, что предельный совокупный доход положителен, убывающий с ростом инвестиций α, то есть

Обозначим через γ ту часть дохода D, которую налогоплательщик укрывает от налогообложения, а через p – вероятность уплаты штрафасвязи с обнаружением этого факта. Пусть k - издержки, обусловленные сокрытием части дохода в размере γD от налогообложения и выраженные в долях этой незадекларированной части дохода; отметим, что в эти издержки входят как комиссионные, уплачиваемые посреднику, так и соответствующие трансакционные издержки, за исключением тех издержек, которые несет налогоплательщик в связи с уплатой штрафа и подкупом чиновников в целях снижения величины p. Пусть t – средняя ставка налога, а f-величина штрафа, выраженная в долях неуплаченного налога 1. Если факт уклонения от налогообложения обнаруживается и влечет за собой штрафные санкции, то налогоплательщик возвращает неуплаченную часть налога в размере tγD, другими словами, в этом случае он уплачивает налог в полном объеме со всего дохода и, дополнительно, уплачивает штраф в размере ftγD.

Сразу заметим, что из предлагаемого подхода может сложиться представление, будто речь идет исключительно о подоходном налоге. Чтобы подобного не произошло, обратим внимание на то, что любой налог так или иначе уплачивается из дохода. Даже в том случае, если речь идет об НДС или акцизах на потребительские товары или импортных пошлинах, продавец, фактически осуществляя передачу соответствующих платежей от покупателя государству, психологически склонен считать, что это именно он несет налоговое бремя, так как ему приходится расставаться с частью своей выручки. Поэтому представляется, что предлагаемый подход применим практически к любому налогу, а не только к подоходному. Просто в подобном случае номинальная ставка того или иного налога должна быть пересчитана применительно к доходу и выражать собой долю дохода, подлежащую уплате.

Для ожидаемой полезности U налогоплательщика с учетом сказанного и в предположении, что он нейтрален к риску, можно написать

В результате элементарных преобразований с использованием обозначения 1+f≡F получим

Выражение (2) полностью соответствует модели В. Вишневского и А. Веткина. Легко видеть, что если в (2) множитель при gamma; (величина в квадратных скобках) положителен, то налогоплательщику выгодно повышать gamma; – долю дохода, укрываемую от налогообложения. И, наоборот, в противном случае налогоплательщик должен снижать γ до нуля, т.е. ему выгодно уплачивать налог со всего получаемого дохода. Фактически в этой модели величина γ может принимать только два дискретных значения: 0 и 1. При самом незначительном изменении параметров, приводящих к изменению знака соответствующего множителя, доля γ сразу меняет свое значение от 0 до 1 или, наоборот, от 1 до 0. Соответственно налогоплательщик сразу переходит из статуса добросовестного налогоплательщика в статус 100%-го «теневика» и наоборот 2. Очевидно, что действительность гораздо богаче, и в реальности укрываемая от налогообложения часть дохода может принимать любые значения в интервале от 0 до 1. Описанная выше ситуация обусловлена недостатком модели, состоящим в том, что в ней не учитывается зависимость вероятности обнаружения факта сокрытия дохода и уплаты штрафа от величины незадекларированного дохода. Действительно, если налогоплательщик уплачивает налог полностью, то он никак не может подвергаться штрафным санкциям за неуплату налога, т.е. если γ = 0, то и вероятность p = 0. Очевидно, что с ростом γ вероятность p при прочих равных условиях увеличивается.

С учетом существования зависимости p от γ найдем, что максимум полезности (2) достигается при следующем значении γ:

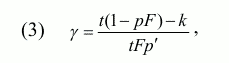
где p&prime – производная от p по γ. Необходимо обратить внимание, что равенство (3) справедливо только в том случае, в котором правая часть не превышает единицу и не меньше нуля. Если же правая часть (3) больше единицы, то γ = 1. Как будет видно из дальнейшего, два случая, отвечающие условиям γ lt; 1 и γ = 1, существенно различаются между собой.

Из (3) можно сделать следующий вывод: величина γ – доля дохода, укрываемая от налогообложения, убывает с ростом k – величины комиссионных выплат и трансакционных издержек 3, с ростом F – уровня штрафных санкций, а также с уменьшением t – ставки налога. Для дальнейшего анализа предположим, что вероятность p линейно зависит от γ и, кроме того, явным образом учтем фактор коррупции в виде возможности налогоплательщика влиять на величину p, иначе говоря, будем считать, что вероятность p убывает с ростом объема взяток, выплачиваемых чиновникам. Используем следующие обозначения:

где n∈(0;1) и характеризует эффективность работы налоговых органов 4 ; h∈(0;1), причем h′ < 0; β – объем инвестиций, направляемых налогоплательщиком в снижение вероятности подвергнуться штрафу за сокрытие доходов. Как видно, величина β может рассматриваться в качестве показателя уровня коррупции.

С учетом (4) из (3) получим, что налогоплательщик максимизирует свою полезность, если выберет следующий уровень сокрытия доходов:

Опять же заметим, что равенство (5) справедливо только в том случае, если правая часть не превышает единицу и не меньше нуля. Предположим сначала, что налогоплательщик укрывает от уплаты налога только часть дохода, другими словами считаем, что γ < 1 и, соответственно, равенство (5) выполняется. Сразу отметим, что в этом случае, как следует из (5), рост величины β, влекущий за собой снижение h, а значит и вероятности уплаты штрафа, оборачивается возрастанием укрываемой от декларирования доли дохода. С учетом (5) выражение для максимальной по γ полезности налогоплательщика принимает вид:

Теперь учтем, что экономический субъект, максимизируя свою полезность, выбирает не только величину недекларируемой части дохода, но и объемы инвестиций, направляемых как в увеличение совокупного дохода, так и в снижение вероятности подвергнуться штрафным санкциям.

Объемы инвестиций, максимизирующие полезность, определяются из условий: U′_α=0 и U′_β=0 , откуда следуют уравнения

Уравнения (7) и (8) легко интерпретировать: предельные доходы субъекта равны его предельным издержкам, так как выражения, стоящие слева от знаков равенства представляют собой предельные по инвестициям α и β доходы экономического субъекта, а стоящие справа единицы выражают собой предельные издержки инвестирования. Из уравнения (7) следует, что уменьшение по тем или иным причинам стоящего во внешних скобках множителя должно компенсироваться увеличением предельного совокупного дохода D′, которое, согласно (1), обусловливается снижением величины инвестирования α, в силу чего в свою очередь происходит понижение величины дохода D. Таким образом, из уравнения (7) следует, что рост комиссионных платежей и трансакционных издержек (рост k), и/или ужесточение наказаний (рост F), и/или повышение эффективности работы налоговых служб (повышение n) снижает стимулы агента к инвестированию в создание стоимости, в результате чего величина совокупного дохода сокращается.

Теперь обратимся к вопросу о влиянии ставки налогообложения на совокупный доход и покажем, что рост налоговой ставки отрицательно влияет на его величину. Для этого достаточно показать, что множитель при D′ в левой части (7) убывает с ростом t. Ради краткости используем для него обозначение:

Легко видеть, что производная от этой функции

принимает неотрицательные значения только в том случае, если выполняется условие

из которого, в частности, следует, что 2nhF <1 Вспомним, что мы рассматриваем случай γ <1, а, значит, из (5) вытекает неравенство

Если бы выполнялось условие (9), то из неравенства (10) следовало бы, что

что противоречит условию (9). Как видим, предположение о неубывающем характере функции x(t) приводит к противоречию. Следовательно, функция x(t) является убывающей. Таким образом, рост ставки налогообложения приводитснижению значения множителя при D′ в левой части уравнения (7), что оборачивается ростом предельного совокупного дохода и, следовательно, уменьшением объема инвестиций α с соответствующим падением величины дохода. И наоборот, снижение налоговой ставки оборачивается возрастание дохода 5, что эквивалентно расширению налогооблагаемой базы. Заметим, что из естественного требования убывания предельной по β полезности, а значит и предельного дохода, из (6) и (8) следует, что величина

является положительной и убывающей по β. Поэтому, в силу уравнения (8), с возрастанием параметра k, и/или n, и/или F происходит рост этой величины (11), что означает снижение β, т.е. снижение уровня коррупции. В этом проявляется рациональность налогоплательщика, который в ответ на возрастание рисков снижает и укрываемую часть дохода, в соответствии с (5), и величину β. Максимизирующий эффект на экономии последней объясняется тем, что, во-первых, с уменьшением γ заинтересованность налогоплательщика в низком значении вероятности p убывает, а во-вторых, снижение γ и так влечет за собой спад вероятности p. Отметим, что в работе В. Вишневского и А. Веткина содержится прямо противоположное утверждение, согласно которому рост размеров штрафа не способствует ни снижения масштабов уклонения от уплаты налогов, ни понижению уровня коррупции. Важно подчеркнуть, что это их утверждение не вытекает из предлагаемой ими же математической модели, а привносится извне, фактически произвольным образом. Тем не менее существуют условия, и ниже они будут указаны, в рамках которых это утверждение оказывается справедливым.

Что же касается влияния ставки налогообложения t, то, согласно (8), ее рост снижает величину (11), что означает рост β, т.е. повышение спроса на коррупцию. Теперь рациональность выбора налогоплательщика выражается в повышении, согласно (5), скрываемой от налогообложения части дохода с одновременным ростом инвестиций в снижение вероятности p, что позволяет уменьшить риски.

Напомним, что полученные выводы справедливы при выполнении условия (5), или другими словами, при 0 < γ < 1. Если же правая часть (5) не меньше единицы, т.е. если при всех рассматриваемых значениях параметров выполняется неравенство

то налогоплательщик укрывает от налогообложения весь доход и, следовательно, γ = 1, p = nh, и выражение для его полезности принимает вид

В этом случае уравнения (7) и (8) сменяются уравнениями

Из уравнения (14) следует, что рост величин k, n, t, F при γ = 1 приводит к увеличению предельного совокупного дохода, которое, как и в случае γ < 1, означает снижение дохода, обусловленное притуплением соответствующих стимулов 6. Отметим, что изменение величины k, согласно уравнению (15), отражается на уровне коррупции только через изменение величины дохода D. Так как рост издержек уклонения от налогообложения приводит к снижению дохода D, которое в силу уравнения (15) оборачивается ростом убывающей по β величины - h′ , то в результате наблюдается снижение спроса на коррупцию. Таким образом, рост величины k и при γ < 1, и при γ = 1 способствует снижению уровня коррупции.

Для того чтобы установить характер влияния на уровень коррупции параметров n, t, F предположим, что наряду с увеличением значений этих параметров происходит такое сокращение k, что величина k+nhtF не изменяется, а значит, согласно (14), сохраняется величина совокупного дохода D. В этом случае, согласно уравнению (15), величина - h′ сокращается, что означает возрастание спроса на коррупцию. В силу сохранения D, мы можем считать, что данное повышение уровня коррупции обусловлено не сокращением величины k, а возрастанием произведения ntF. Следовательно, в отличие от случая γ < 1, при γ = 1 рост n и/или F приводит к росту спроса на коррупцию. И в этом тоже проявляется рациональность налогоплательщика, ибо в условиях возрастающих рисков и укрывания от налогообложения всего дохода он может максимизировать ожидаемую полезность только путем снижения вероятности оказаться подвергнутым штрафным санкциям.

Следует особо подчеркнуть, что уравнения (7)–(8), а также (14)–(15) отвечают оптимальному для налогоплательщика уровню инвестирования, достижение которого предполагает наличие достаточных для этого возможностей. В реальных условиях тех ресурсов, которыми располагает экономический субъект, может оказаться недостаточно для достижения этого уровня. Поэтому полезно рассмотреть случай ограниченных ресурсов. Для этого предположим, что ресурсы, которыми располагает экономический агент, удовлетворяют условию

где I – объем ресурсов, α₀ и &beta₀ – объемы инвестиций, удовлетворяющих уравнениям (7)–(8) или (14)–(15). Считаем, что экономический субъект в условиях ограниченных ресурсов стремится распределить их между двумя видами инвестиций таким образом, чтобы максимизировать свою полезность. Задача, как известно, сводится к отысканию условного максимума полезности при выполнении соответствующего «бюджетного» ограничения (16).

Сначала рассмотрим случай γ < 1 в предположении, что налогоплательщик оптимизирует уровень недекларируемой части дохода в соответствии с (5). Приравняв нулю производные от функции Лагранжа

взятые по α и β, и исключив множитель λ, получим уравнение

согласно которому максимум полезности достигается при условии равенства предельных доходов субъекта по обоим видам инвестиций α и β. Заметим, что согласно уравнениям (7) и (8), предельные доходы и в случае неограниченных7 ресурсов также равны друг другу в силу их равенства соответствующим равным между собой предельным издержкам. В данном же случае ограниченных ресурсов предельные доходы превышают предельные издержки.

Для удобства анализа перепишем уравнение (17) в виде:

Слева в (18) от знака равенства находится зависящая от α функция. Для краткости обозначим ее через y(α). Справа от знака равенства находится функция переменной β. Ее обозначим через z(β). Так как с ростом α доход D возрастает, а предельный доход D′, согласно (1), убывает, то функция y(α) является возрастающей. В силу того что величина (11) является убывающей по β, то обратная величина -h²/h′ , а значит, и величина -h/h′ являются возрастающими по β. Таким образом, функция z(β) также является возрастающей.

На рисунке вертикальные оси y и z расположены на расстоянии I = α + β друг от друга. Переменная α отсчитывается от оси y, находящейся слева, и растет при движении слева направо. Переменная β, наоборот, отсчитывается от осии возрастает при движении справа налево. Точка пересечения графиков функций y(α) и z(β) определяет распределение ресурса I между двумя видами инвестиций α и β.

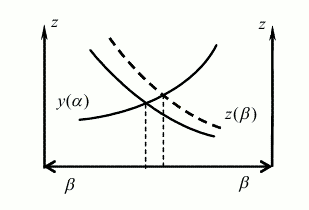
Рис.

Легко видеть, что смещение кривой z(β) вверх, как показано пунктиром на рисунке, приводит к перераспределению ресурсов в пользу величины α. Другими словами, в этом случае уровень коррупции понижается, а инвестиции вповышение совокупного дохода растут, что оборачивается ростом самого дохода. Из уравнения (18) следует, что подобное смещение кривой z(β) обусловлено возрастанием множителя, стоящего в больших скобках. Таким образом, в простейших случаях благоприятное перераспределение ресурсов экономического субъекта достигается в результате возрастания величины n, и/или F, и/или k, либо в результате снижения налоговой ставки t 8.

Обратим внимание на то, что в полном соответствии с выводами В. Вишневского и А. Веткина выражения (5) и (18) указывают на те действия со стороны государства, в результате которых наблюдается рост параметра k, как на элементы наиболее эффективной стратегии борьбы с уклонением налогоплательщика от уплаты налогов. Только повышение издержек k до величины налоговой ставки t способно, как видно из (5), снизить долю γ до нуля. Никаким другим мерам (кроме соответствующего снижения t до уровня k) такой эффект не под силу. Аналогична, как это следует из (18), роль параметра k и в смещении кривой z(β).

Таким образом, повышение ставки налогообложения, как в случае ограниченных ресурсов, так и в случае неограниченных ресурсов влечет за собой ряд отрицательных последствий – растет и укрываемая от налогообложения доля дохода, и спрос на коррупцию с одновременной неблагоприятной деформацией стимулов экономического субъекта и снижением совокупного дохода.

Что же касается остальных параметров, а именно: эффективности работы налоговых служб, издержек уклонения от налогообложения и уровня штрафных санкций, – то их роль при переходе к случаю ограниченных ресурсов сохраняется в отношении уровня коррупции и доли дохода, укрываемой от налогообложения, которые по-прежнему снижаются с ростом перечисленных параметров. Меняется только характер их влияния на величину совокупного дохода: возрастание этих параметров в случае ограниченных ресурсов и увода от налогообложения только части дохода приводит к возрастанию совокупного дохода. Причина такого благотворного влияния кроется в превышении предельных доходов над предельными издержками инвестирования, характерного для условий ограниченных ресурсов. Снижение размеров β позволяет экономическому агенту использовать освободившиеся ресурсы для увеличения инвестиций в повышение совокупного дохода.

Теперь обратимся к случаю сокрытия от налогообложения всего дохода в условии «бюджетного» ограничения (16). Как легко видеть, в этом случае уравнение (18) сменяется уравнением

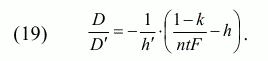
Благоприятное смещение кривой z(β) вверх на рисунке происходит при увеличении множителя в скобках, т.е. при снижении значений параметров k, n, t, F. Таким образом, в этом случае при γ = 1, в отличие от ситуации при γ < 1, рост размера штрафа и/или издержек уклонения от уплаты налогов оборачивается повышением уровня коррупции и снижением совокупного дохода. Несколько неожиданным в этой ситуации представляется повышение уровня коррупции вследствие роста величины k. Объяснение состоит в том, что рост издержек k снижает стимулы для инвестирования в совокупный доход, а так как в условиях ограниченных ресурсов предельные доходы хозяйствующего субъекта превышают предельные издержки инвестирования, то освободившиеся ресурсы инвестируются в снижение вероятности p.

Полученные результаты представлены в таблице. Вертикальная стрелка, стоящая возле латинской или греческой буквы, обозначает увеличение соответствующей величины, если она направлена вверх и, соответственно, снижение, если она направлена вниз. Как видно из последней строки таблицы, ужесточение штрафных санкций способно уменьшить размеры скрываемых от налогообложения доходов. Что же касается уровня коррупции, то однозначный ответ не просматривается: в одних случаях (при γ < 1) рост штрафов способствует сокращению коррупции, в других (при γ = 1), напротив, – его повышению. Неоднозначно влияет на уровень коррупции и повышение издержек уклонения от уплаты налогов. Безусловно, позитивное влияние на все параметры оказывает, как это видно из первой строки таблицы, снижение налоговой ставки. Однако заранее нельзя сказать, как эта мера отразится на бюджете в целом в краткосрочном периоде.

При внимательном рассмотрении таблицы становится очевидным, что случаи полного укрывания доходов от налогообложения (γ = 1) и частичного (γ < 1) требуют к себе различных подходов со стороны государства. При частичном уклонении от налогообложения меры, состоящие и в снижении налоговой ставки, и в повышении издержек уклонения от уплаты налогов, и в возрастании штрафных санкций, и в повышении эффективности работы налоговых служб, приводят к благоприятным последствиям, выра

Выводы, вытекающие из математической модели

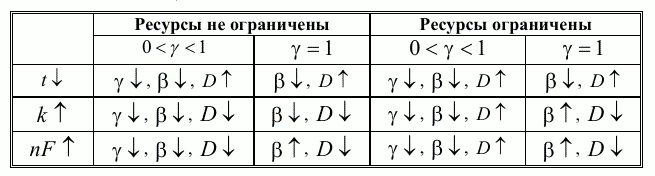
жающимся в снижении как уровня коррупции, так и укрываемой от налогообложения доли доходов. Что же касается случая полного сокрытия дохода от уплаты налогов, то перечисленные меры (кроме одной, состоящей в снижении налоговой ставки) могут приводить к отрицательным последствиям и поэтому обязательно должны предваряться такими мерами, которые способны сначала вывести соответствующую деятельность «из тени» и сделать предпочтительным для налогоплательщика не полное, а частичное укрывание дохода от уплаты налогов. В заключение хотелось бы напомнить, что в настоящей работе рассматривалось поведение только того налогоплательщика, который в той или иной степени утаивает свой доход от налогообложения, другими словами, мы ограничились изучением случая γ > 0, т.е. считали, что, согласно (5), t > k. Очевидно, что при t < k налогоплательщику невыгодно уклоняться от уплаты налогов. В реальности такая ситуация вполне может складываться, например, в отношении налога на недвижимость, налога на наследство или подоходного налога в том случае, в котором доход полностью формируется зарплатой бюджетника 9. В подобных случаях государство может повышать налоговую ставку, не опасаясь ни повышения уровня коррупции, ни возрастания масштабов уклонения от уплаты налогов.

1 В связи с тем, что согласно ст. 198 УК РФ и ст. 122 НК РФ величина штрафа определяется величиной неуплаченного налога, мы, как и авторы вышеуказанной работы, считаем, что размер штрафа пропорционален размеру неуплаченного налога.

2 Вообще говоря, нечто подобное может иметь место. Налогоплательщик может заниматься различными видами деятельности или осуществлять трансакции на различных сегментах рынка. В тех случае, когда соответствующий множитель меньше нуля, он может вести себя как честный налогоплательщик, а в других – полностью скрывать свой доход. Например, так может поступать врач, оказывающий дополнительные платные услуги, преподаватель, занимающийся репетиторством, фирма, занимающаяся ремонтом квартир или бытовой техники и т.п.

3 Механизмы повышения издержек уклонения от налогообложения подробно рассматриваются в упомянутой работе В. Вишневского, А. Веткина.

4 Коэффициент n отражает зависимость эффективности работы налоговых органов от тех условий, которые мы здесь специально не оговариваем. Его величина зависит от частоты и тщательности осуществляемых налоговыми органами проверок. Кроме того, его значения могут сильно различаться на различных сегментах рынка. Например, преподаватель школы или вуза может совмещать официальную работу с оказываемыми в частном порядке репетиторскими услугами. Если в первом случае информация о его доходах открыта для налоговых органов и, соответственно, значение n близко к единице, то во втором случае его доходы документально не фиксируются и, соответственно, n близко к нулю.

5 Отметим, что в простейшем случае добросовестного налогоплательщика, т.е. при γ = 0, уравнение (7) принимает вид (1 – t)D′=1, из которого сразу следует, что снижение ставки налогообложения приводит к уменьшению предельного дохода D′, что означает рост дохода D.

6 У читателя может возникнуть следующий вопрос: если экономический субъект полностью скрывает свой доход от налогообложения, то каким образом может возникать зависимость его стимулов и полного дохода от ставки налогообложения? Дело в том, что от величины налоговой ставки t, как видно из (14) и (15), зависит ожидаемый размер штрафа. Поэтому рост t при прочих равных условиях влечет рост издержек и, соответственно, притупление стимулов к инвестированию в повышение дохода при одновременном, как будет видно из дальнейшего, возрастании стимулов к инвестированию в снижение вероятности p.

7 Напомним, что под неограниченными ресурсами подразумевается возможность выполнения условий (7)–(8) или (14)–(15).

8 Конечно же, благоприятное смещение кривой z(β) и соответствующее перераспределение инвестиционных потоков возможно не только в этих случаях. Множитель, стоящий в больших скобках в выражении (18), может возрасти и в том случае, если, к примеру, отрицательное влияние роста налоговой ставки t будет скомпенсировано достаточным для этого увеличением параметра k, и/или F, и/или n. Для государства дешевле всего, конечно, увеличивать F. Отсюда следует, например, что переход к прогрессивной подоходной шкале должен сопровождаться соответствующим ростом внимания к более высоким доходам, причем в отношении возрастающего дохода должен быть предусмотрен рост не просто размера штрафа за уклонение от налогообложения в денежном выражении, а рост его уровня (величины F), выраженного в долях неуплаченного налога.

9 Естественно считать, что если налогоплательщик получает зарплату в бюджетной организации, то его издержки уклонения от уплаты подоходного налога весьма велики.